problem
stringlengths 10
7.44k
| answer
stringlengths 1
270
| difficulty
stringclasses 8
values |
|---|---|---|
## G3
Let $C D \perp A B(D \in A B), D M \perp A C(M \in A C)$ and $D N \perp B C(N \in B C)$ for an acute triangle ABC with area $S$. If $H_{1}$ and $H_{2}$ are the orthocentres of the triangles $M N C$ and MND respectively. Evaluate the area of the quadrilateral $\mathrm{AH}_{1} \mathrm{BH}_{2}$.
|
S
|
5/8
|
Alex, Pei-Hsin, and Edward got together to send a mailing to all the invited schools. Pei-Hsin stuffs and sometimes licks the envelopes. If Alex leaves the room, Pei-Hsin has a $25 \%$ chance of dying from an allergic reaction and a $20 \%$ chance of being killed by Edward before licking the envelopes. Alex leaves the room and comes back to find Pei-Hsin dead. What is the probability that Edward was responsible?
|
\dfrac{1}{2}
|
3/8
|
770. It is required to divide the segment $\boldsymbol{A} \boldsymbol{B}$ in half. How should the radii of the arcs described from points $\boldsymbol{A}$ and $\boldsymbol{B}$, as centers, be chosen so that the construction is as accurate as possible?
|
\dfrac{AB}{\sqrt{2}}
|
0/8
|
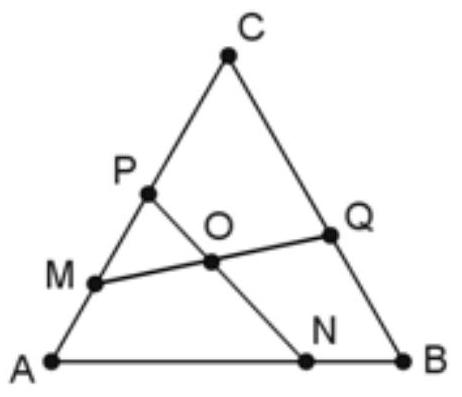
5. In an equilateral triangle $ABC$ with side length $a$, points $M, N, P, Q$ are positioned as shown in the figure. It is known that $MA + AN = PC + CQ = a$. Find the measure of angle $NOQ$.
|
60^\circ
|
2/8
|
Let $m\ge 3$ and $n$ be positive integers such that $n>m(m-2)$. Find the largest positive integer $d$ such that $d\mid n!$ and $k\nmid d$ for all $k\in\{m,m+1,\ldots,n\}$.
|
m-1
|
1/8
|
11. In a convex hexagon $A B C D E F$ with 6 equal sides, the interior angles $A, B, C$ are $134^{\circ}, 106^{\circ}, 134^{\circ}$, respectively. Then the interior angle $E$ is $\qquad$
(Answer in degrees)
|
134
|
4/8
|
Class $\mathbf{M}$.
In the class, there are 15 boys and 15 girls. On March 8, some boys called some girls to congratulate them on the holiday (no boy called the same girl twice). It turned out that the children could be uniquely divided into 15 pairs so that in each pair there was a boy who called the girl. What is the maximum number of calls that could have been made?
|
120
|
4/8
|
Three. (50 points) Given $n$ as a positive integer no less than 2. For all non-negative arrays $a_{i}(i=1,2, \cdots, n)$, find the maximum value of $\frac{\left(\sum_{i=1}^{n} i a_{i}\right)\left(\sum_{i=1}^{n} \frac{a_{i}}{i}\right)}{\left(\sum_{i=1}^{n} a_{i}\right)^{2}}$.
|
\dfrac{(n+1)^2}{4n}
|
4/8
|
Arnold thought of 5 numbers and told Bendegúz all the possible sums obtained by adding any two of these numbers. These sums are: $6, 7, 8, 8, 9, 9, 10, 10, 11, 12$. What were the numbers that Arnold thought of?
|
\{2.5, 3.5, 4.5, 5.5, 6.5\}
|
0/8
|
4. Two odd natural numbers $k$ and $n$ are given. Martin wrote the fraction $i / j$ on the board for each pair of natural numbers $i, j$ satisfying $1 \leqq i \leqq k$ and $1 \leqq j \leqq n$. Determine the median of all these fractions, that is, such a real number $q$ that if all the fractions on the board are arranged in ascending order by value (fractions with the same value in any order), the fraction in the middle of this list will have the value $q$. (Martin Melicher)
|
\dfrac{k+1}{n+1}
|
4/8
|
Task 3. (15 points) Lab engineer Dasha received an object for research consisting of about 100 monoliths (a container designed for 100 monoliths, which was almost completely filled). Each monolith has a specific name (sandy loam or clayey loam) and genesis (marine or lake-glacial deposits). The relative frequency (statistical probability) that a randomly selected monolith will be sandy loam is $\frac{1}{7}$. The relative frequency that a randomly selected monolith will be marine clayey loam is $\frac{9}{14}$. How many monoliths of lake-glacial genesis does the object contain, if there are no marine sandy loams among the sandy loams?
#
|
35
|
5/8
|
12. (10 points) Cut a pentagon along a straight line into two polygons, then cut one of the polygons along a straight line into two parts, resulting in three polygons, and then cut one of the polygons along a straight line into two parts, $\cdots$, and so on. To have 20 pentagons among the resulting polygons, what is the minimum number of cuts needed?
|
38
|
1/8
|
Task 1. Two cars covered the same distance. The speed of the first was constant and three times less than the initial speed of the second. The second car traveled the first half of the distance without changing its speed, then it suddenly reduced its speed by half, traveled another quarter of the distance at a constant speed, and then again reduced its speed by half, traveling another eighth of the distance at a constant speed, and so on. After the eighth reduction in speed, it did not change its speed until the end of the trip. How many times more time did the second car need to cover the entire distance compared to the first?
|
\dfrac{5}{3}
|
5/8
|
1.1. A group of tourists set out on a route from a campsite. After 15 minutes, tourist Ivan remembered that he had forgotten a flashlight at the campsite and went back for it at a higher speed than the main group. After picking up the flashlight, he started to catch up with the group at the same increased speed and did so only 2.5 hours after he left to get the flashlight. Assuming the speeds of the group and Ivan outside the group are constant, find how many times Ivan's speed is greater than the group's speed. Write the answer as an integer or a decimal.
|
1.2
|
4/8
|
4. From Zlatoust to Miass, "GAZ", "MAZ", and "KamAZ" set off simultaneously. "KamAZ", having reached Miass, immediately turned back and met "MAZ" 18 km from Miass, and "GAZ" - 25 km from Miass. "MAZ", having reached Miass, also immediately turned back and met "GAZ" 8 km from Miass. What is the distance from Zlatoust to Miass
|
60
|
4/8
|
Carl only eats food in the shape of equilateral pentagons. Unfortunately, for dinner he receives a piece of steak in the shape of an equilateral triangle. So that he can eat it, he cuts off two corners with straight cuts to form an equilateral pentagon. The set of possible perimeters of the pentagon he obtains is exactly the interval \([a, b)\), where \(a\) and \(b\) are positive real numbers. Compute \(\frac{a}{b}\).
|
4\sqrt{3}-6
|
0/8
|
A regular hexagon is drawn on the plane with a side length of 1. Using only a ruler, construct a segment whose length is $\sqrt{7}$.
|
\sqrt{7}
|
4/8
|
Father has left several identical gold coins to his children. According to his will, the oldest child receives one coin and one-seventh of the remaining coins, the next child receives two coins and one-seventh of the remaining coins, the third child receives three coins and one-seventh of the remaining coins, and so on through the youngest child. If every child inherits an integer number of coins, find the number of children and the number of coins.
|
36
|
3/8
|
Suppose we have a convex polygon in which all interior angles are integers when measured in degrees, and the interior angles at every two consecutive vertices differ by exactly \(1^{\circ}\). If the greatest and least interior angles in the polygon are \(M^{\circ}\) and \(m^{\circ}\), what is the maximum possible value of \(M - m\)?
|
18
|
1/8
|
There are 54 drivers employed in a garage. How many days off can each driver have in a month (30 days), if every day 25% of the 60 cars are in the garage for preventive maintenance?
|
5
|
3/8
|
A domino has a left end and a right end, each of a certain color. Alice has four dominos, colored red-red, red-blue, blue-red, and blue-blue. Find the number of ways to arrange the dominos in a row end-to-end such that adjacent ends have the same color. The dominos cannot be rotated.
|
4
|
5/8
|
There are 4 numbers written on a board. Vasya multiplied the first of these numbers by \(\sin \alpha\), the second by \(\cos \alpha\), the third by \(\operatorname{tg} \alpha\), and the fourth by \(\operatorname{ctg} \alpha\) (for some angle \(\alpha\)) and obtained a set of the same 4 numbers (possibly in a different order). What is the maximum number of distinct numbers that could have been written on the board?
|
3
|
1/8
|
Two signals, $A$ and $B$, are transmitted over a communication line with probabilities of 0.72 and 0.28, respectively. Due to noise, $\frac{1}{6}$ of $A$ signals are distorted and received as $B$ signals, and $\frac{1}{7}$ of transmitted $B$ signals are received as $A$ signals.
a) Determine the probability that an $A$ signal will be received at the receiving end.
b) Given that an $A$ signal is received, what is the probability that it was originally transmitted as an $A$ signal?
|
0.9375
|
0/8
|
In a movie theater, 80% of the adults are men. Among the male audience, 40% are children. Additionally, 20% of the children are boys. What is the minimum number of people watching the movie?
|
55
|
5/8
|
There are 5 houses, numbered 1 to 5 from left to right, as seen from across the street. Each house is occupied by a different person. Each house has a unique attribute for each of the following characteristics:
- Each person has a unique name: `Alice`, `Peter`, `Eric`, `Arnold`, `Bob`
- Each person has a unique birthday month: `sept`, `mar`, `april`, `feb`, `jan`
- The people keep unique animals: `horse`, `bird`, `dog`, `fish`, `cat`
## Clues:
1. The person whose birthday is in September is Peter.
2. The dog owner is in the first house.
3. Bob is not in the second house.
4. The bird keeper is not in the second house.
5. The bird keeper is not in the fourth house.
6. The person whose birthday is in March is not in the second house.
7. Bob and the person whose birthday is in January are next to each other.
8. The person who keeps horses is the person whose birthday is in February.
9. Eric is in the first house.
10. The person whose birthday is in March and the person whose birthday is in April are next to each other.
11. The bird keeper is not in the third house.
12. The cat lover is not in the second house.
13. Arnold is in the fourth house.
What is the value of attribute Birthday for the person whose attribute House is 1? Please reason step by step, and put your final answer within \boxed{}
|
mar
|
0/8
|
There are 5 houses, numbered 1 to 5 from left to right, as seen from across the street. Each house is occupied by a different person. Each house has a unique attribute for each of the following characteristics:
- Each person has a unique name: `Bob`, `Alice`, `Eric`, `Arnold`, `Peter`
- Each mother is accompanied by their child: `Meredith`, `Bella`, `Timothy`, `Fred`, `Samantha`
- They all have a unique favorite flower: `tulips`, `roses`, `lilies`, `daffodils`, `carnations`
## Clues:
1. The person who loves a bouquet of daffodils is not in the first house.
2. The person's child is named Fred is Bob.
3. The person's child is named Fred is not in the second house.
4. The person's child is named Fred is somewhere to the left of the person who loves a carnations arrangement.
5. Peter is not in the first house.
6. The person's child is named Fred and the person who loves the boquet of lilies are next to each other.
7. Arnold is the person who is the mother of Timothy.
8. The person's child is named Bella is somewhere to the right of Eric.
9. The person who is the mother of Timothy is not in the first house.
10. Eric is the person who loves the boquet of lilies.
11. There is one house between the person's child is named Meredith and the person's child is named Fred.
12. The person who loves the vase of tulips is in the second house.
What is the value of attribute Flower for the person whose attribute Children is Timothy? Please reason step by step, and put your final answer within \boxed{}
|
tulips
|
1/8
|
There are 3 houses, numbered 1 to 3 from left to right, as seen from across the street. Each house is occupied by a different person. Each house has a unique attribute for each of the following characteristics:
- Each person has a unique name: `Eric`, `Arnold`, `Peter`
- Each person prefers a unique type of vacation: `mountain`, `city`, `beach`
- People have unique heights: `very short`, `average`, `short`
- They all have a unique favorite flower: `carnations`, `daffodils`, `lilies`
- People have unique hair colors: `brown`, `black`, `blonde`
- Each person has a unique level of education: `associate`, `bachelor`, `high school`
## Clues:
1. Peter is the person who has an average height.
2. The person who loves a bouquet of daffodils is Arnold.
3. The person who is very short is not in the second house.
4. The person who loves beach vacations is in the first house.
5. The person with a high school diploma is in the third house.
6. The person who is short is somewhere to the right of the person who is very short.
7. The person who loves the boquet of lilies is Eric.
8. The person who loves the boquet of lilies is the person with a bachelor's degree.
9. The person who prefers city breaks is somewhere to the right of Peter.
10. The person who has blonde hair is in the third house.
11. The person who loves beach vacations is the person who has brown hair.
What is the value of attribute Vacation for the person whose attribute Education is associate? Please reason step by step, and put your final answer within \boxed{}
|
mountain
|
3/8
|
There are 6 houses, numbered 1 to 6 from left to right, as seen from across the street. Each house is occupied by a different person. Each house has a unique attribute for each of the following characteristics:
- Each person has a unique name: `Eric`, `Arnold`, `Carol`, `Bob`, `Peter`, `Alice`
- Each person lives in a unique style of house: `ranch`, `victorian`, `modern`, `colonial`, `craftsman`, `mediterranean`
- Each person has a unique favorite drink: `coffee`, `water`, `root beer`, `tea`, `milk`, `boba tea`
- Each person has an occupation: `engineer`, `nurse`, `doctor`, `artist`, `lawyer`, `teacher`
- The people keep unique animals: `horse`, `fish`, `dog`, `cat`, `rabbit`, `bird`
- Each person has a favorite color: `red`, `purple`, `white`, `green`, `yellow`, `blue`
## Clues:
1. The fish enthusiast is in the first house.
2. Carol is somewhere to the left of the person in a Mediterranean-style villa.
3. The bird keeper is the person who loves purple.
4. The person in a ranch-style home is the one who only drinks water.
5. The coffee drinker is not in the fourth house.
6. The person living in a colonial-style house and the boba tea drinker are next to each other.
7. The cat lover is the person who is a teacher.
8. The person in a modern-style house is in the third house.
9. The person who is an engineer and Peter are next to each other.
10. Arnold is the person who is an artist.
11. The person whose favorite color is red is Arnold.
12. The coffee drinker is somewhere to the right of the person who is a teacher.
13. The bird keeper is the person in a ranch-style home.
14. The rabbit owner is in the sixth house.
15. The boba tea drinker is Peter.
16. Eric is the cat lover.
17. The person who is a nurse is directly left of the person in a modern-style house.
18. The bird keeper is Carol.
19. There are two houses between the cat lover and the boba tea drinker.
20. Bob is the tea drinker.
21. The person residing in a Victorian house is the dog owner.
22. The person whose favorite color is green is in the fourth house.
23. The person who loves blue is the root beer lover.
24. The person who loves white is not in the sixth house.
25. Peter is the person who is a doctor.
What is the value of attribute Animal for the person whose attribute Occupation is engineer? Please reason step by step, and put your final answer within \boxed{}
|
horse
|
0/8
|
There are 4 houses, numbered 1 to 4 from left to right, as seen from across the street. Each house is occupied by a different person. Each house has a unique attribute for each of the following characteristics:
- Each person has a unique name: `Arnold`, `Eric`, `Peter`, `Alice`
- Each person has a unique level of education: `master`, `high school`, `associate`, `bachelor`
- Everyone has something unique for lunch: `stew`, `grilled cheese`, `pizza`, `spaghetti`
- People have unique favorite sports: `soccer`, `swimming`, `tennis`, `basketball`
- People have unique hair colors: `blonde`, `black`, `brown`, `red`
- People have unique favorite book genres: `mystery`, `fantasy`, `science fiction`, `romance`
## Clues:
1. The person who loves the stew is in the first house.
2. The person who loves science fiction books is the person who has black hair.
3. The person who has blonde hair is not in the second house.
4. The person with a master's degree is in the first house.
5. Eric is the person who loves soccer.
6. The person with a master's degree and the person who loves mystery books are next to each other.
7. The person who loves tennis is the person with a high school diploma.
8. The person who loves the spaghetti eater is the person who loves science fiction books.
9. The person who is a pizza lover is the person with an associate's degree.
10. The person who has blonde hair is not in the fourth house.
11. The person with a master's degree is directly left of Eric.
12. The person with a bachelor's degree is directly left of the person who loves fantasy books.
13. The person who has red hair is Peter.
14. The person who loves swimming is directly left of the person who is a pizza lover.
15. Alice is not in the first house.
What is the value of attribute FavoriteSport for the person whose attribute BookGenre is mystery? Please reason step by step, and put your final answer within \boxed{}
|
soccer
|
0/8
|
There are 4 houses, numbered 1 to 4 from left to right, as seen from across the street. Each house is occupied by a different person. Each house has a unique attribute for each of the following characteristics:
- Each person has a unique name: `Alice`, `Eric`, `Arnold`, `Peter`
- Each person has a unique hobby: `painting`, `gardening`, `photography`, `cooking`
- People have unique favorite book genres: `romance`, `science fiction`, `mystery`, `fantasy`
- Each person prefers a unique type of vacation: `city`, `beach`, `mountain`, `cruise`
- People have unique favorite music genres: `rock`, `pop`, `classical`, `jazz`
- Each person has a unique level of education: `high school`, `associate`, `bachelor`, `master`
## Clues:
1. The person who loves science fiction books is somewhere to the right of the person who loves fantasy books.
2. The person who paints as a hobby is the person who loves fantasy books.
3. Arnold is the person who loves fantasy books.
4. The person with a high school diploma is the person who loves pop music.
5. The person who loves cooking is somewhere to the right of Eric.
6. There are two houses between the photography enthusiast and the person who loves beach vacations.
7. The person who loves romance books is Peter.
8. The person who enjoys mountain retreats is not in the second house.
9. The person with a bachelor's degree is somewhere to the right of the person with a high school diploma.
10. The person who loves classical music is not in the third house.
11. The person who prefers city breaks is the person who loves science fiction books.
12. The person who loves rock music is Peter.
13. The person with a bachelor's degree is not in the fourth house.
14. The person with a master's degree is the person who loves jazz music.
15. The person who enjoys gardening is the person who loves romance books.
What is the value of attribute BookGenre for the person whose attribute MusicGenre is rock? Please reason step by step, and put your final answer within \boxed{}
|
romance
|
1/8
|
There are 5 houses, numbered 1 to 5 from left to right, as seen from across the street. Each house is occupied by a different person. Each house has a unique attribute for each of the following characteristics:
- Each person has a unique name: `Bob`, `Alice`, `Eric`, `Arnold`, `Peter`
- Each mother is accompanied by their child: `Meredith`, `Bella`, `Timothy`, `Fred`, `Samantha`
- They all have a unique favorite flower: `tulips`, `roses`, `lilies`, `daffodils`, `carnations`
## Clues:
1. The person who loves a bouquet of daffodils is not in the first house.
2. The person's child is named Fred is Bob.
3. The person's child is named Fred is not in the second house.
4. The person's child is named Fred is somewhere to the left of the person who loves a carnations arrangement.
5. Peter is not in the first house.
6. The person's child is named Fred and the person who loves the boquet of lilies are next to each other.
7. Arnold is the person who is the mother of Timothy.
8. The person's child is named Bella is somewhere to the right of Eric.
9. The person who is the mother of Timothy is not in the first house.
10. Eric is the person who loves the boquet of lilies.
11. There is one house between the person's child is named Meredith and the person's child is named Fred.
12. The person who loves the vase of tulips is in the second house.
What is the value of attribute House for the person whose attribute Name is Eric? Please reason step by step, and put your final answer within \boxed{}
|
4
|
0/8
|
There are 4 houses, numbered 1 to 4 from left to right, as seen from across the street. Each house is occupied by a different person. Each house has a unique attribute for each of the following characteristics:
- Each person has a unique name: `Peter`, `Eric`, `Arnold`, `Alice`
- People have unique favorite music genres: `pop`, `classical`, `jazz`, `rock`
- Each person has a unique hobby: `cooking`, `gardening`, `painting`, `photography`
- Each person has a unique level of education: `master`, `associate`, `high school`, `bachelor`
- Each person has a unique type of pet: `fish`, `bird`, `dog`, `cat`
## Clues:
1. The person who loves classical music is not in the fourth house.
2. Arnold is the person with a master's degree.
3. Alice is the person who owns a dog.
4. The person who enjoys gardening is not in the third house.
5. The person with a bachelor's degree is Alice.
6. Alice is the photography enthusiast.
7. Arnold is directly left of the person who loves pop music.
8. The person with an associate's degree is directly left of the photography enthusiast.
9. The person who loves rock music is the person who loves cooking.
10. The person with an associate's degree is Eric.
11. The person who has a cat is the person who loves jazz music.
12. Arnold is somewhere to the right of the person with an aquarium of fish.
What is the value of attribute Education for the person whose attribute Hobby is painting? Please reason step by step, and put your final answer within \boxed{}
|
master
|
0/8
|
There are 5 houses, numbered 1 to 5 from left to right, as seen from across the street. Each house is occupied by a different person. Each house has a unique attribute for each of the following characteristics:
- Each person has a unique name: `Peter`, `Alice`, `Arnold`, `Bob`, `Eric`
- The people are of nationalities: `swede`, `norwegian`, `brit`, `german`, `dane`
- Everyone has something unique for lunch: `stew`, `grilled cheese`, `stir fry`, `pizza`, `spaghetti`
- Everyone has a favorite smoothie: `desert`, `lime`, `watermelon`, `cherry`, `dragonfruit`
## Clues:
1. Alice is the person who likes Cherry smoothies.
2. The person who drinks Lime smoothies is the person who loves eating grilled cheese.
3. The Dragonfruit smoothie lover is somewhere to the right of the person who loves the stew.
4. The German is Bob.
5. The person who loves stir fry is somewhere to the right of Eric.
6. Arnold is directly left of the Dane.
7. The person who loves the spaghetti eater is the Norwegian.
8. Bob is somewhere to the left of the person who drinks Lime smoothies.
9. The Desert smoothie lover is the person who is a pizza lover.
10. The German is somewhere to the right of the Norwegian.
11. The Swedish person is the person who is a pizza lover.
12. There is one house between the person who loves eating grilled cheese and Peter.
What is the value of attribute House for the person whose attribute Name is Alice? Please reason step by step, and put your final answer within \boxed{}
|
1
|
0/8
|
There are 6 houses, numbered 1 to 6 from left to right, as seen from across the street. Each house is occupied by a different person. Each house has a unique attribute for each of the following characteristics:
- Each person has a unique name: `Peter`, `Carol`, `Eric`, `Alice`, `Bob`, `Arnold`
- People use unique phone models: `huawei p50`, `google pixel 6`, `xiaomi mi 11`, `iphone 13`, `samsung galaxy s21`, `oneplus 9`
- Everyone has a unique favorite cigar: `dunhill`, `pall mall`, `blends`, `blue master`, `prince`, `yellow monster`
- They all have a unique favorite flower: `daffodils`, `carnations`, `roses`, `tulips`, `lilies`, `iris`
- Each person has a favorite color: `yellow`, `red`, `green`, `blue`, `white`, `purple`
- People have unique favorite sports: `soccer`, `tennis`, `basketball`, `volleyball`, `swimming`, `baseball`
## Clues:
1. The person who uses a OnePlus 9 is in the second house.
2. The person who uses a Xiaomi Mi 11 is somewhere to the left of the person who uses a Huawei P50.
3. Carol is the person who loves a carnations arrangement.
4. The person who loves purple is directly left of the person partial to Pall Mall.
5. The person whose favorite color is green is the person who smokes Blue Master.
6. The person who loves yellow and the person who loves blue are next to each other.
7. Eric is somewhere to the right of the person who uses a Samsung Galaxy S21.
8. There are two houses between Carol and the person who loves a bouquet of daffodils.
9. The Prince smoker is the person who loves basketball.
10. The Dunhill smoker is the person who loves volleyball.
11. The person who loves swimming is the person who uses a Google Pixel 6.
12. The person who uses a Huawei P50 is directly left of the person who loves white.
13. The person who uses a OnePlus 9 and the person who loves the rose bouquet are next to each other.
14. The person who loves the boquet of iris is somewhere to the left of Eric.
15. The Dunhill smoker is Peter.
16. The person who loves blue is Peter.
17. The person who loves the vase of tulips is Bob.
18. Alice is in the first house.
19. The person who loves baseball is directly left of the person who smokes Blue Master.
20. The person who uses a Google Pixel 6 is somewhere to the right of the person who smokes many unique blends.
21. The person who loves soccer is Carol.
22. The person who loves a carnations arrangement is directly left of the person who smokes many unique blends.
23. Eric is the person who smokes many unique blends.
24. The person who loves volleyball is the person who uses an iPhone 13.
What is the value of attribute Flower for the person whose attribute FavoriteSport is swimming? Please reason step by step, and put your final answer within \boxed{}
|
tulips
|
0/8
|
There are 4 houses, numbered 1 to 4 from left to right, as seen from across the street. Each house is occupied by a different person. Each house has a unique attribute for each of the following characteristics:
- Each person has a unique name: `Alice`, `Peter`, `Eric`, `Arnold`
- Each person has an occupation: `doctor`, `teacher`, `engineer`, `artist`
- Each mother is accompanied by their child: `Meredith`, `Fred`, `Bella`, `Samantha`
- Everyone has something unique for lunch: `spaghetti`, `pizza`, `stew`, `grilled cheese`
## Clues:
1. The person who loves the spaghetti eater is directly left of the person who is a teacher.
2. Arnold is somewhere to the left of the person's child is named Samantha.
3. The person's child is named Bella is in the first house.
4. The person who loves the spaghetti eater is directly left of Peter.
5. The person who loves the stew is Arnold.
6. The person who is an artist is the person who is a pizza lover.
7. Arnold is the person who is an engineer.
8. Alice is the person's child is named Samantha.
9. The person who is a doctor is not in the first house.
10. The person's child is named Meredith is not in the fourth house.
11. Eric is the person's child is named Bella.
What is the value of attribute Food for the person whose attribute Name is Peter? Please reason step by step, and put your final answer within \boxed{}
|
grilled cheese
|
1/8
|
There are 6 houses, numbered 1 to 6 from left to right, as seen from across the street. Each house is occupied by a different person. Each house has a unique attribute for each of the following characteristics:
- Each person has a unique name: `Peter`, `Eric`, `Arnold`, `Bob`, `Alice`, `Carol`
- The people keep unique animals: `rabbit`, `dog`, `fish`, `bird`, `cat`, `horse`
- Each person has a unique hobby: `cooking`, `knitting`, `painting`, `woodworking`, `photography`, `gardening`
- People have unique favorite sports: `basketball`, `soccer`, `swimming`, `tennis`, `baseball`, `volleyball`
- Each person prefers a unique type of vacation: `cruise`, `cultural`, `city`, `camping`, `mountain`, `beach`
- Each person has a unique favorite drink: `water`, `root beer`, `boba tea`, `tea`, `milk`, `coffee`
## Clues:
1. The person who enjoys camping trips is the person who loves cooking.
2. The person who loves baseball is the photography enthusiast.
3. The person who loves volleyball is somewhere to the left of the person who prefers city breaks.
4. Carol is the person who loves tennis.
5. The dog owner is the person who loves swimming.
6. The photography enthusiast is the tea drinker.
7. The person who loves baseball is directly left of the person who goes on cultural tours.
8. Peter is the person who enjoys camping trips.
9. The person who enjoys knitting is the person who keeps horses.
10. The coffee drinker is directly left of the person who loves soccer.
11. The person who enjoys mountain retreats is the person who loves soccer.
12. The boba tea drinker is not in the fourth house.
13. The cat lover is somewhere to the left of the dog owner.
14. The person who loves beach vacations is Bob.
15. The coffee drinker is somewhere to the right of Alice.
16. The tea drinker is the fish enthusiast.
17. The person who likes milk is Carol.
18. There is one house between the rabbit owner and the woodworking hobbyist.
19. The person who loves cooking is not in the third house.
20. The person who loves tennis is the rabbit owner.
21. The dog owner is directly left of the person who likes going on cruises.
22. The woodworking hobbyist is the dog owner.
23. There are two houses between the person who paints as a hobby and the person who keeps horses.
24. Arnold is the root beer lover.
What is the value of attribute Vacation for the person whose attribute Drink is root beer? Please reason step by step, and put your final answer within \boxed{}
|
mountain
|
0/8
|
There are 6 houses, numbered 1 to 6 from left to right, as seen from across the street. Each house is occupied by a different person. Each house has a unique attribute for each of the following characteristics:
- Each person has a unique name: `Alice`, `Bob`, `Carol`, `Peter`, `Eric`, `Arnold`
- The mothers' names in different houses are unique: `Holly`, `Sarah`, `Penny`, `Kailyn`, `Aniya`, `Janelle`
## Clues:
1. Carol is somewhere to the right of Bob.
2. The person whose mother's name is Aniya is in the first house.
3. Eric is in the second house.
4. Peter is The person whose mother's name is Penny.
5. There is one house between Peter and Carol.
6. The person whose mother's name is Holly is somewhere to the left of Arnold.
7. The person whose mother's name is Sarah and The person whose mother's name is Penny are next to each other.
8. The person whose mother's name is Sarah is not in the fifth house.
9. The person whose mother's name is Janelle is Bob.
10. The person whose mother's name is Sarah is not in the second house.
What is the value of attribute Mother for the person whose attribute Name is Arnold? Please reason step by step, and put your final answer within \boxed{}
|
Sarah
|
1/8
|
There are 6 houses, numbered 1 to 6 from left to right, as seen from across the street. Each house is occupied by a different person. Each house has a unique attribute for each of the following characteristics:
- Each person has a unique name: `Eric`, `Bob`, `Alice`, `Peter`, `Arnold`, `Carol`
- They all have a unique favorite flower: `daffodils`, `carnations`, `roses`, `tulips`, `iris`, `lilies`
- People have unique heights: `very tall`, `super tall`, `average`, `short`, `very short`, `tall`
- Each person has a favorite color: `blue`, `yellow`, `purple`, `red`, `green`, `white`
- Everyone has a unique favorite cigar: `yellow monster`, `pall mall`, `prince`, `blue master`, `blends`, `dunhill`
- People use unique phone models: `google pixel 6`, `iphone 13`, `xiaomi mi 11`, `samsung galaxy s21`, `huawei p50`, `oneplus 9`
## Clues:
1. The person who uses an iPhone 13 is the person who loves white.
2. Peter is the person whose favorite color is red.
3. The Prince smoker is directly left of the person partial to Pall Mall.
4. The person who smokes Blue Master and the Dunhill smoker are next to each other.
5. The person who loves blue is the person who uses a Xiaomi Mi 11.
6. The person who loves white is Alice.
7. The person who uses a OnePlus 9 is somewhere to the left of Arnold.
8. The person who is tall is the person who smokes Blue Master.
9. The person who uses a Samsung Galaxy S21 is the Dunhill smoker.
10. Bob is directly left of the person who is very short.
11. The person who loves a bouquet of daffodils is Eric.
12. The person who loves the boquet of iris is the person who uses a OnePlus 9.
13. The person who uses a Huawei P50 is the person who is very short.
14. The person who smokes many unique blends is directly left of Peter.
15. The Prince smoker is not in the first house.
16. The person who is very tall is the person who loves a bouquet of daffodils.
17. The person who uses a Google Pixel 6 is not in the fifth house.
18. The person who is tall is not in the third house.
19. The person who uses a Huawei P50 is somewhere to the left of the person who uses a Samsung Galaxy S21.
20. Arnold is somewhere to the left of the person who is short.
21. The person who loves the vase of tulips is not in the first house.
22. The person who loves the boquet of lilies is directly left of the person who loves yellow.
23. Arnold is the person who loves purple.
24. The person who uses a OnePlus 9 and the person who uses a Samsung Galaxy S21 are next to each other.
25. The person who has an average height is not in the first house.
26. The person who loves the rose bouquet is Alice.
What is the value of attribute Color for the person whose attribute Cigar is yellow monster? Please reason step by step, and put your final answer within \boxed{}
|
white
|
0/8
|
There are 6 houses, numbered 1 to 6 from left to right, as seen from across the street. Each house is occupied by a different person. Each house has a unique attribute for each of the following characteristics:
- Each person has a unique name: `Peter`, `Arnold`, `Eric`, `Alice`, `Bob`, `Carol`
- Everyone has a favorite smoothie: `dragonfruit`, `cherry`, `lime`, `desert`, `blueberry`, `watermelon`
- Each person has a unique type of pet: `rabbit`, `fish`, `bird`, `hamster`, `cat`, `dog`
- Each person has a unique level of education: `master`, `bachelor`, `high school`, `trade school`, `associate`, `doctorate`
- People have unique heights: `short`, `very tall`, `very short`, `tall`, `average`, `super tall`
## Clues:
1. The person with an aquarium of fish is in the first house.
2. The person with a doctorate is somewhere to the left of the person who owns a dog.
3. Peter and the person with a high school diploma are next to each other.
4. There is one house between the person with a pet hamster and the person who owns a rabbit.
5. The person who has a cat is Eric.
6. Bob and the person who owns a dog are next to each other.
7. The person who is tall is Carol.
8. The person with a master's degree is the person with a pet hamster.
9. Peter is the person who is very tall.
10. The person who likes Cherry smoothies is the person who is very tall.
11. The person who is super tall is somewhere to the right of Arnold.
12. The Watermelon smoothie lover is in the sixth house.
13. The person who is super tall is the Desert smoothie lover.
14. The person who is very short is the person with an associate's degree.
15. The person with an associate's degree and the Watermelon smoothie lover are next to each other.
16. The person who drinks Lime smoothies is the person with a pet hamster.
17. The person who is short is in the second house.
18. The person who drinks Blueberry smoothies is the person who attended trade school.
19. The person who is very short is somewhere to the right of Bob.
What is the value of attribute Smoothie for the person whose attribute House is 2? Please reason step by step, and put your final answer within \boxed{}
|
lime
|
0/8
|
There are 6 houses, numbered 1 to 6 from left to right, as seen from across the street. Each house is occupied by a different person. Each house has a unique attribute for each of the following characteristics:
- Each person has a unique name: `Arnold`, `Bob`, `Eric`, `Carol`, `Alice`, `Peter`
- Each person has a unique level of education: `doctorate`, `trade school`, `associate`, `high school`, `bachelor`, `master`
- People own unique car models: `chevrolet silverado`, `ford f150`, `honda civic`, `tesla model 3`, `bmw 3 series`, `toyota camry`
- Each person has a unique favorite drink: `tea`, `water`, `boba tea`, `coffee`, `root beer`, `milk`
- They all have a unique favorite flower: `carnations`, `iris`, `lilies`, `tulips`, `daffodils`, `roses`
## Clues:
1. Eric is the one who only drinks water.
2. The person with an associate's degree is the person who owns a Toyota Camry.
3. The boba tea drinker is in the fourth house.
4. The person who loves the vase of tulips is directly left of the person who owns a Tesla Model 3.
5. The person with a master's degree is somewhere to the left of the person who owns a BMW 3 Series.
6. The person who owns a Toyota Camry is directly left of the person who loves a bouquet of daffodils.
7. The person who loves the boquet of iris is somewhere to the left of the root beer lover.
8. The person who likes milk is somewhere to the right of the person who owns a Honda Civic.
9. Carol is the person who owns a Honda Civic.
10. The person with a high school diploma is in the second house.
11. The person with a master's degree is the boba tea drinker.
12. The person who owns a Tesla Model 3 is Arnold.
13. The person who loves the boquet of lilies is the person who owns a Tesla Model 3.
14. The person who loves a carnations arrangement is somewhere to the left of Alice.
15. The person with a bachelor's degree is somewhere to the right of the person who likes milk.
16. The one who only drinks water is the person who owns a Ford F-150.
17. Carol is somewhere to the left of the person with a doctorate.
18. There are two houses between the person who owns a Toyota Camry and the person who loves the vase of tulips.
19. The person who owns a Tesla Model 3 is somewhere to the left of the coffee drinker.
20. Bob is in the third house.
What is the value of attribute Education for the person whose attribute Drink is water? Please reason step by step, and put your final answer within \boxed{}
|
high school
|
0/8
|
There are 5 houses, numbered 1 to 5 from left to right, as seen from across the street. Each house is occupied by a different person. Each house has a unique attribute for each of the following characteristics:
- Each person has a unique name: `Arnold`, `Eric`, `Peter`, `Bob`, `Alice`
- Everyone has a favorite smoothie: `watermelon`, `lime`, `cherry`, `dragonfruit`, `desert`
- The people keep unique animals: `fish`, `bird`, `horse`, `cat`, `dog`
- Each person prefers a unique type of vacation: `camping`, `beach`, `mountain`, `city`, `cruise`
- Each person has a unique favorite drink: `root beer`, `water`, `milk`, `tea`, `coffee`
## Clues:
1. The person who keeps horses is the person who drinks Lime smoothies.
2. There is one house between the Watermelon smoothie lover and the person who likes Cherry smoothies.
3. Bob and the coffee drinker are next to each other.
4. The fish enthusiast is the one who only drinks water.
5. The bird keeper is Bob.
6. The person who enjoys mountain retreats is directly left of the root beer lover.
7. The person who loves beach vacations is somewhere to the left of the dog owner.
8. Eric is the person who likes Cherry smoothies.
9. The tea drinker is Alice.
10. The person who prefers city breaks is somewhere to the right of the person who enjoys mountain retreats.
11. Peter is somewhere to the left of the coffee drinker.
12. Eric is the person who loves beach vacations.
13. The person who enjoys mountain retreats is Alice.
14. There are two houses between the Watermelon smoothie lover and Alice.
15. The person who enjoys camping trips is not in the first house.
16. The dog owner is not in the fifth house.
17. The fish enthusiast and the Dragonfruit smoothie lover are next to each other.
What is the value of attribute Drink for the person whose attribute Name is Alice? Please reason step by step, and put your final answer within \boxed{}
|
tea
|
0/8
|
There are 6 houses, numbered 1 to 6 from left to right, as seen from across the street. Each house is occupied by a different person. Each house has a unique attribute for each of the following characteristics:
- Each person has a unique name: `Carol`, `Eric`, `Bob`, `Peter`, `Arnold`, `Alice`
- Each person prefers a unique type of vacation: `cultural`, `beach`, `mountain`, `cruise`, `camping`, `city`
- The people are of nationalities: `chinese`, `brit`, `norwegian`, `swede`, `dane`, `german`
- Everyone has a favorite smoothie: `lime`, `desert`, `watermelon`, `blueberry`, `dragonfruit`, `cherry`
## Clues:
1. The person who likes Cherry smoothies is the person who enjoys mountain retreats.
2. Eric is the Dane.
3. The German is Peter.
4. The Desert smoothie lover is in the sixth house.
5. The Swedish person is the Dragonfruit smoothie lover.
6. Arnold is the Dragonfruit smoothie lover.
7. The Watermelon smoothie lover is the British person.
8. The Norwegian is the person who enjoys camping trips.
9. The person who likes going on cruises is the British person.
10. There are two houses between Bob and the person who enjoys camping trips.
11. The person who drinks Blueberry smoothies is directly left of the person who goes on cultural tours.
12. Bob is directly left of the Dragonfruit smoothie lover.
13. The person who likes going on cruises is directly left of Peter.
14. The person who prefers city breaks is not in the sixth house.
15. Carol is in the fifth house.
What is the value of attribute Vacation for the person whose attribute Name is Eric? Please reason step by step, and put your final answer within \boxed{}
|
mountain
|
0/8
|
There are 6 houses, numbered 1 to 6 from left to right, as seen from across the street. Each house is occupied by a different person. Each house has a unique attribute for each of the following characteristics:
- Each person has a unique name: `Carol`, `Bob`, `Arnold`, `Peter`, `Alice`, `Eric`
- People have unique favorite book genres: `mystery`, `fantasy`, `science fiction`, `romance`, `historical fiction`, `biography`
## Clues:
1. Carol is directly left of Arnold.
2. Eric is the person who loves mystery books.
3. The person who loves romance books and the person who loves science fiction books are next to each other.
4. Peter is somewhere to the right of the person who loves historical fiction books.
5. Arnold is somewhere to the right of the person who loves fantasy books.
6. There is one house between the person who loves biography books and Arnold.
7. The person who loves romance books is not in the sixth house.
8. The person who loves mystery books is not in the sixth house.
9. Alice is the person who loves science fiction books.
10. Carol is in the second house.
What is the value of attribute House for the person whose attribute BookGenre is biography? Please reason step by step, and put your final answer within \boxed{}
|
1
|
0/8
|
LeRoy paid $L$ dollars, Bernardo paid $B$ dollars, and Cecilia paid $C$ dollars, where $L < B < C$. Calculate the amount in dollars that LeRoy must give to Cecilia so that they share the costs equally.
|
\frac{B + C - 2L}{3}
|
3/8
|
A frog starts at point $(2, 3)$ on a grid and makes jumps of length $1$ parallel to the coordinate axes. Each jump direction (up, down, right, or left) is chosen randomly. The jumping sequence stops when the frog reaches any point on the boundary of the rectangle defined by vertices $(0,0), (0,5), (5,5),$ and $(5,0)$. Calculate the probability that the sequence of jumps ends at either the top or bottom horizontal side of the rectangle.
|
\frac{1}{2}
|
0/8
|
Given nine squares are arranged in a 3x3 grid and numbered from 1 to 9 from left to right, top to bottom. The paper is folded three times in sequence: fold the right third over to the middle third, fold the left third over the previous fold covering the right and middle thirds, and fold the bottom third up to the top third. Determine the numbered square that ends up on top after these folds.
|
7
|
1/8
|
Cameron has $90$ red tokens and $60$ blue tokens. He can exchange three red tokens for one gold token and two blue tokens, or two blue tokens for one gold token and one red token. What is the total number of gold tokens Cameron ends up with after exchanging his tokens until no more exchanges can be made?
|
148
|
4/8
|
Jack had a bag of $150$ apples. He sold $20\%$ of them to Jill. Next, he sold $30\%$ of the remaining apples to June. Afterwards, he decides to sell $10\%$ of what's left to Jeff. Finally, Jack donates $5\%$ of the remaining apples to a local school. What is the number of apples that Jack has left after all these transactions?
|
72
|
3/8
|
A hemisphere with a radius of 3 rests on the base of a triangular pyramid of height 9, and the hemisphere is tangent to all three faces of the pyramid. Calculate the length of each side of the base of the equilateral triangle.
|
6\sqrt{3}
|
1/8
|
Let $x$ be the number of students in Mina's high school. Given that Nina's high school has 5 times as many students as Mina's high school, the number of students in Nina's high school is $5x$. Furthermore, if 200 students were to transfer from Nina's high school to Mina's high school, the total number of students in Mina's high school would be $x+200$ and the total number of students in Nina's high school, after the transfer, would be $5x-200$. The problem states that after the transfer, the two schools would have twice as many students as the smaller school. Therefore, the equation $2(x+200) = 5x-200$ can be formed. Solving for $x$, we find that $x=800. Thus, there are $\boxed{4000}$ students in Nina's high school.
|
4000
|
3/8
|
A rectangular board of 10 rows is numbered in a snaking pattern, starting in the upper left corner. In the first row, the squares are numbered from 1 to 10, in the second row from 20 to 11 (backwards), and so on alternating directions each row. A student shades square 1, then skips one square and shades square 3, skips two squares and shades square 6, skips three squares and shades square 10, continuing in this manner. Determine the number of the shaded square that is the first to ensure at least one shaded square in each row.
|
91
|
2/8
|
A tetrahedron has 4 vertices. You choose three vertices at random to form a triangle.
|
1
|
1/8
|
A regular hexagon $ABCDEF$ with side length 2 has two circles positioned outside it. The first circle is tangent to $\overline{AB}$ and the second circle is tangent to $\overline{CD}$. Both circles are also tangent to lines $BC$ and $FA$. Find the ratio of the area of the second circle to that of the first circle.
|
1
|
1/8
|
A beam of light originates from point $A$ on a plane and is reflected several times between lines $AD$ and $CD$ before finally striking a point $B$ on line $CD$ at a $15^\circ$ angle and then reflecting back to point $A$. If the angle $\measuredangle CDA=10^\circ$, determine the maximum number of times the light can be reflected before striking $B$.
|
8
|
1/8
|
10.298. Determine the area of the segment if its perimeter is $p$, and the arc contains $120^{\circ}$.
|
\dfrac{3(4\pi - 3\sqrt{3})}{4(3\sqrt{3} + 2\pi)^2} p^2
|
0/8
|
II. (25 points) As shown in the figure, on the sides $AB$ and $CD$ of a square $ABCD$ with side length 1, points $M$ and $N$ are taken respectively. $AN$ and $DM$ intersect at $E$, and $BN$ and $CM$ intersect at $F$. Try to find the maximum area of quadrilateral $EMFN$, and indicate the positions of $M$ and $N$ when this maximum value can be achieved.
|
\dfrac{1}{4}
|
4/8
|
$\left[\begin{array}{l}\text { B } \quad \text { Inscribed and Circumscribed Circles } \\ \text { [Trigonometric Ratios in a Right Triangle] }\end{array}\right.$
In triangle $ABC$, a circle with center $O$ is inscribed. The line $BO$ intersects this circle at points $M$ and $N$, and the segments $AO$ and $CO$ intersect the circle at points $P$ and $Q$, respectively. Find the ratio of the areas of triangles $MNP$ and $MQN$, if $\angle A=\alpha, \angle C=\gamma$.
|
\dfrac{\cos \frac{\gamma}{2}}{\cos \frac{\alpha}{2}}
|
4/8
|
Example 7 In an acute triangle $\triangle ABC$, the circumcenter is $O$. The midpoints of segments $OA$ and $BC$ are $M$ and $N$ respectively, $\angle ABC = 4 \angle OMN$, and $\angle ACB = 6 \angle OMN$. Find $\angle OMN$.
(1995 Japan Olympiad Problem)
|
12^\circ
|
3/8
|
A convex $n$-gon $P$, where $n > 3$, is dissected into equal triangles by diagonals non-intersecting inside it. Which values of $n$ are possible, if $P$ is circumscribed?
|
4
|
5/8
|
3. Xiao Li and Xiao Zhang are running at a constant speed on a circular track. They start from the same place at the same time. Xiao Li runs clockwise and completes a lap every 72 seconds, while Xiao Zhang runs counterclockwise and completes a lap every 80 seconds. At the start, Xiao Li has a relay baton, and each time they meet, the baton is passed from one to the other (the time taken for passing the baton is negligible). The relay baton returns to the starting point in the minimum of $\qquad$ seconds.
|
720
|
4/8
|
Consider the numbers $1, 2, \ldots, n$ and form $n \times n$ matrices (called "squares") with the property that each number appears exactly once in each row and each column. For $n=2$, examples of such squares are:
\[
\begin{matrix}
1 & 2 \\
2 & 1
\end{matrix} \quad \text{and} \quad
\begin{matrix}
2 & 1 \\
1 & 2
\end{matrix}.
\]
For $n=3$, examples are:
\[
\begin{matrix}
1 & 2 & 3 \\
2 & 3 & 1 \\
3 & 1 & 2
\end{matrix} \quad \text{and} \quad
\begin{matrix}
1 & 2 & 3 \\
3 & 1 & 2 \\
2 & 3 & 1
\end{matrix}.
\]
Let $L_{n}$ be the number of Latin squares of size $n \times n$.
Show that
\[
L_{n} \geq n!(n-1)!\ldots 1! \quad \left(=\prod_{k=1}^{n} k!\right).
\]
It is challenging to find exact formulas for $L_{n}$. (Specific values are $L_{2}=2$, $L_{3}=12$, $L_{4}=576$.) Asymptotically, it is known that
\[
\ln L_{n} = n^{2} \ln n + O(n^{2}), \quad n \rightarrow \infty.
\]
|
L_{n} \geq \prod_{k=1}^{n} k!
|
2/8
|
46. The lateral faces of a triangular pyramid are equal in area and are inclined to the base plane at angles $\alpha, \beta$, and $\gamma$. Find the ratio of the radius of the sphere inscribed in this pyramid to the radius of the sphere that touches the base of the pyramid and the extensions of the three lateral faces.
|
\dfrac{3 - \cos \alpha - \cos \beta - \cos \gamma}{3 + \cos \alpha + \cos \beta + \cos \gamma}
|
0/8
|
12. After removing one element from the set $\{1!, 2!, \cdots, 24!\}$, the product of the remaining elements is exactly a perfect square.
|
12!
|
1/8
|
6. Given $x, y, z \in \mathbf{R}_{+}$, and $s=\sqrt{x+2}+\sqrt{y+5}+\sqrt{z+10}, t=\sqrt{x+1}+\sqrt{y+1}+$ $\sqrt{z+1}$, then the minimum value of $s^{2}-t^{2}$ is $\qquad$ .
|
36
|
4/8
|
Katka cut out 20 rectangles from paper. The first one had dimensions $1 \mathrm{~cm} \times 2 \mathrm{~cm}$, the second $2 \mathrm{~cm} \times 3 \mathrm{~cm}$, the third $3 \mathrm{~cm} \times 4 \mathrm{~cm}$, and so on. Then she started folding them together with the same length sides, ensuring they did not overlap and no rectangle touched more than two other rectangles.
a) Draw the polygon that Katka formed from the first six of her rectangles.
b) Determine the perimeter of Katka's polygon formed from all the cut-out rectangles.
|
462
|
1/8
|
13. Sarah and Hagar play a game of darts. Let $O_{0}$ be a circle of radius 1. On the $n$th turn, the player whose turn it is throws a dart and hits a point $p_{n}$ randomly selected from the points of $O_{n-1}$. The player then draws the largest circle that is centered at $p_{n}$ and contained in $O_{n-1}$, and calls this circle $O_{n}$. The player then colors every point that is inside $O_{n-1}$ but not inside $O_{n}$ her color. Sarah goes first, and the two players alternate turns. Play continues indefinitely. If Sarah's color is red, and Hagar's color is blue, what is the expected value of the area of the set of points colored red?
|
\dfrac{6}{7} \pi
|
2/8
|
Let $n$ be a positive integer. A frog starts on the number line at 0 . Suppose it makes a finite sequence of hops, subject to two conditions:
- The frog visits only points in $\left\{1,2, \ldots, 2^{n}-1\right\}$, each at most once.
- The length of each hop is in $\left\{2^{0}, 2^{1}, 2^{2}, \ldots\right\}$. (The hops may be either direction, left or right.)
Let $S$ be the sum of the (positive) lengths of all hops in the sequence. What is the maximum possible value of $S$ ?
|
\dfrac{4^n -1}{3}
|
2/8
|
9. The integers from 1 to $n$ are written in increasing order from left to right on a blackboard. David and Goliath play the following game: starting with David, the two players alternate erasing any two consecutive numbers and replacing them with their sum or product. Play continues until only one number on the board remains. If it is odd, David wins, but if it is even, Goliath wins. Find the 2011th smallest positive integer greater than 1 for which David can guarantee victory.
|
4022
|
2/8
|
13. (GDR 1) Find whether among all quadrilaterals whose interiors lie inside a semicircle of radius \( r \) there exists one (or more) with maximal area. If so, determine their shape and area.
|
\dfrac{3\sqrt{3}}{4} r^2
|
4/8
|
On a $(4 n+2) \times(4 n+2)$ square grid, a turtle can move between squares sharing a side. The turtle begins in a corner square of the grid and enters each square exactly once, ending in the square where she started. In terms of $n$, what is the largest positive integer $k$ such that there must be a row or column that the turtle has entered at least $k$ distinct times?
|
2n + 2
|
3/8
|
7. In the tetrahedron $SABC$, $\triangle ABC$ is an equilateral triangle. The projection of point $A$ onto the plane $SBC$ is $H$, which is the orthocenter of $\triangle SBC$. The dihedral angle $H-AB-C$ has a plane angle of $30^{\circ}$, and $SA=2\sqrt{3}$. What is the volume of the tetrahedron $SABC$?
|
\dfrac{9\sqrt{3}}{4}
|
1/8
|
Given the natural $n$. We shall call [i]word [/i] sequence from $n$ letters of the alphabet, and [i]distance [/i] $\rho(A, B)$ between [i]words [/i] $A=a_1a_2\dots a_n$ and $B=b_1b_2\dots b_n$ , the number of digits in which they differ (that is, the number of such $i$, for which $a_i\ne b_i$). We will say that the [i]word [/i] $C$ [i]lies [/i] between words $A$ and $B$ , if $\rho (A,B)=\rho(A,C)+\rho(C,B)$. What is the largest number of [i]words [/i] you can choose so that among any three, there is a [i]word lying[/i] between the other two?
|
2^{n}
|
0/8
|
[ Combinatorics (miscellaneous).]
$[$ Estimation + example $]$
In a pond, 30 pikes were released, which gradually eat each other. A pike is considered full if it has eaten at least three pikes (full or hungry). What is the maximum number of pikes that can become full?
|
9
|
0/8
|
5. How many four-digit numbers exist that have the following properties: all digits of the number are even; the number is divisible by four, if the last digit is erased, the resulting three-digit number is not divisible by four?
|
120
|
3/8
|
In space, there are four distinct points, $A, B, C$, and $D$. We know that there is an isometry of space that swaps $A$ and $B$, and leaves $C$ and $D$ fixed; furthermore, there is an isometry that maps $A$ to $B$, $B$ to $C$, $C$ to $D$, and $D$ to $A$. What is the measure of angle $ABC$? And what is the measure of angle $DAC$?
|
60^\circ
|
1/8
|
A square $ABCD$ has side length $ 1$. A circle passes through the vertices of the square. Let $P, Q, R, S$ be the midpoints of the arcs which are symmetrical to the arcs $AB$, $BC$, $CD$, $DA$ when reflected on sides $AB$, $B$C, $CD$, $DA$, respectively. The area of square $PQRS$ is $a+b\sqrt2$, where $a$ and $ b$ are integers. Find the value of $a+b$.
[img]https://cdn.artofproblemsolving.com/attachments/4/3/fc9e1bd71b26cfd9ff076db7aa0a396ae64e72.png[/img]
|
1
|
2/8
|
Let $\triangle ABC$ be a right triangle with hypotenuse $AC$. A square is inscribed in the triangle such that points $D,E$ are on $AC$, $F$ is on $BC$, and $G$ is on $AB$. Given that $AG=2$ and $CF=5$, what is the area of $\triangle BFG$?
|
\dfrac{500}{841}
|
0/8
|
8. Let $A=\left\{a_{1}, a_{2}, \cdots, a_{7}\right\}$. Here $a_{i} \in \mathbf{Z}^{\prime}$, and let $n_{A}$ denote the number of triples $(x, y, z)$ such that: $x<y$, $x+y=z, x, y, z \in A$. Then the maximum possible value of $n_{A}$ is $\qquad$.
|
9
|
2/8
|
16. A competition consists of $n$ true/false questions. Statistics on the answers of 8 candidates show that: for any two questions, exactly two candidates answer “ $T, T$ ”; exactly two candidates answer “ $F, F$ ”; exactly two candidates answer “ $T, F$ ”; exactly two candidates answer “ $F, T$ ”. Find the maximum value of $n$.
|
7
|
1/8
|
1. A university has 10001 students, some of whom join and form several clubs (a student can belong to different clubs), and some clubs join together to form several associations (a club can belong to different associations). It is known that there are $k$ associations in total. Assume the following conditions are met:
(1) Every pair of students (i.e., any two students) belong to exactly one club;
(2) For each student and each association, the student belongs to exactly one club of that association;
(3) Each club has an odd number of students, and a club with $2m$ +1 students belongs to exactly $m$ associations, where $m$ is a positive integer.
Find all possible values of $k$.
|
5000
|
4/8
|
3. Problem: You have an unlimited supply of square tiles with side length 1 and equilateral triangle tiles with side length 1 . For which $n$ can you use these tiles to create a convex $n$-sided polygon? The tiles must fit together without gaps and may not overlap.
|
3 \leq n \leq 12
|
0/8
|
## Task A-4.3.
On the edge of a square, a total of $4 n$ points are marked: all four vertices of the square and an additional $n-1$ points on each side of the square. Determine the number of all (non-degenerate) triangles for which the marked points are vertices.
|
10n^3 - 8n^2 + 2n
|
5/8
|
Question 155, The edge length of the regular tetrahedron $\mathrm{ABCD}$ is 2, the angle $\theta$ between edge $\mathrm{AD}$ and plane $\alpha$ is $\theta \in\left[\frac{\pi}{3}, \frac{\pi}{2}\right]$, and vertex $\mathrm{A}$ is on plane $\alpha$, while B, C, D are all outside of $\alpha$. Find the range of the distance from the midpoint $\mathrm{E}$ of edge $\mathrm{BC}$ to plane $\alpha$.
|
\left[ \dfrac{\sqrt{3} - \sqrt{2}}{2}, \dfrac{\sqrt{3} + \sqrt{2}}{2} \right]
|
1/8
|
10. Among the positive integers less than 10000, by swapping the digits in the highest and lowest positions of a number, a new number is obtained, and this new number is 1.2 times the original number. The sum of all numbers that satisfy the above condition is $\qquad$ .
|
5535
|
3/8
|
11. Let $A_{1}, A_{2}, \ldots, A_{11}$ be 11 points on a straight line in order, where $A_{1} A_{11}=56$. Given that $A_{i} A_{i+2} \leq 12$ for $i=1,2, \ldots, 9$ and $A_{j} A_{j+3} \geq 17$ for $j=1,2, \ldots, 8$, find $A_{2} A_{7}$.
Let $A_{1}, A_{2}, \ldots, A_{11}$ be 11 points on a straight line in order, where $A_{1} A_{11}=56$. Given that $A_{i} A_{i+2} \leq 12$ for $i=1,2, \ldots, 9$ and $A_{j} A_{j+3} \geq 17$ for $j=1,2, \ldots, 8$, find $A_{2} A_{7}$.
|
29
|
2/8
|
Example 3. Find the integral $\int \operatorname{sh}^{2} x \operatorname{ch}^{2} x d x$.
|
\dfrac{1}{32} \sinh 4x - \dfrac{x}{8} + C
|
0/8
|
Seregay I.n.
Inside triangle $A B C$, a point $O$ is taken such that $\angle A B O=\angle C A O, \angle B A O=\angle B C O, \angle B O C=90^{\circ}$. Find the ratio $A C: O C$.
|
\sqrt{2}
|
2/8
|
The Planar National Park is an undirected 3-regular planar graph (i.e., all vertices have degree 3). A visitor walks through the park as follows: she begins at a vertex and starts walking along an edge. When she reaches the other endpoint, she turns left. On the next vertex she turns right, and so on, alternating left and right turns at each vertex. She does this until she gets back to the vertex where she started. What is the largest possible number of times she could have entered any vertex during her walk, over all possible layouts of the park?
|
3
|
3/8
|
Example 4. Given $\triangle A B C$ and a line $D E$ parallel to $B C$ intersecting at points $B D E$, the area of $\triangle B D E$ equals $k^{2}$. Then, what is the relationship between $k^{2}$ and the area $S$ of $\triangle A B C$ for the problem to have a solution? How many solutions are there?
(1987, Shanghai)
|
k^2 \leq \frac{S}{4}
|
3/8
|
A-5. Find the maximum value of the following expression:
$$
\int_{0}^{y} \sqrt{x^{4}+\left(y-y^{2}\right)^{2}} d x \text {, }
$$
where $0 \leqslant y \leqslant \mathrm{i}$.
|
\dfrac{1}{3}
|
4/8
|
136. The square root of half the bee swarm flew to a jasmine bush. Eight ninths of the swarm stayed at home. One bee flew after the male, worried by his buzzing in a lotus flower, where he had ended up at night, attracted by the pleasant fragrance, and cannot get out as the flower has closed. Tell me the number of bees in the swarm.
|
72
|
2/8
|
An urn contains $n$ white and $n$ black balls. We draw them without replacement, but before doing so, we must predict the outcomes of all the draws. What is the expected number of correct predictions?
|
n
|
4/8
|
6. In trapezoid $\mathrm{PQRS}$, it is known that $\angle \mathrm{PQR}=90^{\circ}, \angle Q R S>90^{\circ}$, diagonal $S Q$ is 24 and is the bisector of angle $S$, and the distance from vertex $R$ to line $Q S$ is 5. Find the area of trapezoid PQRS.
|
\dfrac{27420}{169}
|
2/8
|
3. In triangle $A B C$, angle $A$ is equal to $60^{\circ}$, the distances from vertices $B$ and $C$ to the center of the inscribed circle of triangle $A B C$ are 3 and 4, respectively. Find the radius of the circle circumscribed around triangle $A B C$.
|
\dfrac{\sqrt{111}}{3}
|
5/8
|
Let $a$ be a positive real numbers. Let $t,\ u\ (t<u)$ be the $x$ coordinates of the point of intersections of the curves : $C_1:y=|\cos x|\ (0\leq x\leq \pi),\ C_2:y=a\sin x\ (0\leq x\leq \pi).$ Denote by $S_1$ the area of the part bounded by $C_1,\ C_2$ and $y$-axis in $0\leq x\leq t$, and by $S_2$ the area of the part bounded by $C_1,\ C_2$ in $t\leq x\leq u$. When $a$ moves over all positive real numbers, find the minimum value of $S_1+S_2$.
|
2\sqrt{2} - 2
|
4/8
|
Three, (25 points) Let $x, y (x>y)$ be any two numbers in a set of distinct natural numbers $a_{1}, a_{2}, \cdots, a_{n}$, satisfying $x-y \geqslant \frac{xy}{31}$. Find the maximum value of the number of elements $n$ in this set of natural numbers.
|
10
|
2/8
|
13.7.5 ** Given the parabola $y^{2}=2 p x(p>0)$, two perpendicular chords $F A$ and $F B$ are drawn through the focus $F$ of the parabola. Find the minimum value of the area of $\triangle F A B$.
|
(3 - 2\sqrt{2})p^2
|
1/8
|
Example 13. A regular octagon inscribed in a circle has four adjacent sides of length 2, and the other four sides of length 3. Find the area of this octagon.
|
13 + 12\sqrt{2}
|
5/8
|
9. Arrange the sequence of numbers
$$
\sqrt{2}, 2, \sqrt{6}, 2 \sqrt{2}, \sqrt{10}, \cdots, 10 \sqrt{2}
$$
in the following manner:
\begin{tabular}{ccccc}
$\sqrt{2}$ & 2 & $\sqrt{6}$ & $2 \sqrt{2}$ & $\sqrt{10}$ \\
$2 \sqrt{3}$ & $\sqrt{14}$ & 4 & $3 \sqrt{2}$ & $2 \sqrt{5}$ \\
$\sqrt{22}$ & $2 \sqrt{6}$ & $\cdots$ & $\cdots$ & $\cdots$ \\
$\vdots$ & & & & $\vdots$ \\
$\cdots$ & $\cdots$ & $\cdots$ & $\cdots$ & $10 \sqrt{2}$
\end{tabular}
According to this arrangement, the position of $3 \sqrt{2}$ can be denoted as $(2, 4)$, and the position of $2 \sqrt{6}$ can be denoted as $(3, 2)$. Therefore, the position of the largest rational number in this sequence, according to this arrangement, can be denoted as
|
(20,3)
|
1/8
|
3. On the line AB, point O is marked and from it rays OC, OD, OE, OF are drawn in the specified order into one half-plane of line AB (ray OC lies between rays OA and OD). Find the sum of all angles with vertex O, whose sides are rays OA, OC, OD, OE, OF, OB, if $\angle \mathrm{COF}=97^{\circ}, \angle \mathrm{DOE}=35^{\circ}$.
|
1226
|
1/8
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.